از حسن توجه شما سپاسگزارم!

 

«معادله دیفرانسیل»

مقدمه

معادله دیفرانسیل معادله‌ای است که شامل یک یا چند مشتق یا دیفرانسیل باشد. معادلات دیفرانسیل بر اساس ویژگیهای زیر رده بندی می‌شوند:

نوع (عادی یا جزئی)

• معادله شامل متغیر مستقل x ، تابع (y = f(x و مشتقات f را یک معادله دیفرانسیل عادی می‌نامیم.
   
• معادله ای متشکل از یک تابع مجهول با بیش از یک متغیر مستقل همراه با مشتقات جزئی آن معادله دیفرانسیل جزئی می نامیم.

مرتبه

که عباترت است از مرتبه مشتقی که بالاترین مرتبه را در معادله دارد.

درجه

نمای بالاترین توان مشتقی که بالاترین مرتبه را در معادله دارد، پس از حذف مخرج کسرها و رادیکالهای مربوط به متغیر وابسته و مشتقاتش. معمولا یک معادله دیفرانسیل مرتبه n جوابی شامل n ثابت دلخواه دارد، این جواب را جواب عمومی می‌نامند.

ساختار

معادلات دیفرانسیل ساختارهای متفاوتی هستند و هر ساختار ویژگیهای متفاوتی دارد:

 

• معادلات مرتبه اول از درجه اول
  • با متغیرهای جدایی پذیر
  • همگن
  • خطی (برنولی)
  • با دیفرانسیلهای کامل
• معادلات مرتبه دوم
• معادلات خطی با ضرایب ثابت: الف) همگن ب) ناهمگن.
• تکنیکهای تقریب زدن: الف) سریهای توانی ب) روشهای عددی.

صور مختلف معادلات دیفرانسیل

معادله دیفرانسیل مرتبه اول از درجه اول را همواره می‌توان به صورت زیر در آورد که در آن M و N معرف توابعی از x و y هستند.

 

Mdx + Ndy = 0

در معادله فوق هرگاه M فقط تابعی از x و N فقط تابعی از y باشد. به صورت معادله جدایی پذیر مرتبه اول است. در این صورت با انتگرال گیری از هر جمله جواب بدست می‌آید. یعنی:

 

M(x) dx+ ∫N(y) dy = C∫

 

ادامه نوشته

«معادله درجه چهارم»

در ریاضیات معادلهٔ درجهٔ چهار عبارتی است که بتواند به صورت تساوی یک تابع درجه چهار با صفر بیان شود. فرم عمومی تابع درجهٔ چهار به صورت زیر است:

 

به طوریکه a ≠ ۰.

معادله ای با درجهٔ بیشتر از چهار که بتوان آن را به وسیلهٔ ریشه‌های عددی حل کرد وجود ندارد و درجهٔ چهار بالاترین درجه ای است که می‌توان آن را به وسیلهٔ ریشهٔ عددی حل کرد.

 

تاریخچه

لودوویکو فراری مشهور به کشف روش حل معادلهٔ درجهٔ چهار است. او در سال ۱۵۴۰ راه حل آن را کشف کرد اما این راه حل مانند باقی راه حل‌های حل معادلهٔ درجه چهار مستلزم کشف راه حل معادلات درجهٔ سه بودند. بالاخره جرلامو کاردانو استاد فراری راه حل معادلهٔ درجهٔ چهار همراه با راه حل معادله ی درجه سه در کتاب Ars Magna (1545) منتشر کرد.

«معادله درجه سوم»

در ریاضیات، معادله درجه 3 یک چند جمله‌ای است که بیشترین درجه مجهول آن 3 باشد. به عنوان مثال معادله یک معادله درجه 3 می‌باشد، فرم کلی معادلات درجه سوم به صورت نوشته می‌شود. که بطور معمول ضرایب معادله‌ای را حقیقی هستند. همچنین، همواره منفی بر اینست که در چنین معادله‌ای باشد. حل معادله‌ درجه سوم متوجه پیدا کردن ریشه‌های معادله می‌باشد.

 

تاریخچه

معادلات درجه سوم برای اولین بار توسط ریاضیدانان هندسی در حدود 400 سال قبل از میلاد مورد توجه قرار گرفت. در بین ریاضیدانان پارسی، عمر خیام (1123-1048) راه حلی را برای حل معادله درجه سوم ابداع کرد. او در این روش با استفاده از هندسه نشان داد که چگونه با استفاده از روش هندسی می‌توان به جواب عددی معادله رسید با استفاده از جدول مثلثاتی. همچنین در حول و حوش قرن 16، یک ریاضیدان ایتالیایی به نام scipione، روشی را برای حل کلاسی از معادلات درجه سوم که به صورت 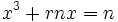می‌باشند را ادامه داد. او همچنین نشان داد که تمامی معادلات درجه سوم را می‌توان به صورت گفته شده کاهش داد.

ادامه نوشته

«معادله درجه دوم»

تعریف

دایره ، سهمی ، بیضی و هذلولی هستند که معادله‌شان حالت‌های خاصی از معادله درجه دوم زیر است:

 

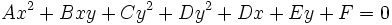
بطور مثال دایره: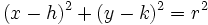

 

-

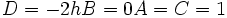
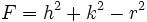از معادله درجه دوم فوق بدست آورد. در واقع خط راست هم حالت خاصی از معادله درجه دوم است هرگاه 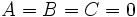ولی این شرایط معادله درجه دوم را به یک معادله خطی بجای معادله درجه دوم بدل می‌کنند جملات 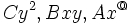جملات درجه دوم می‌باشند و در حال حاضر رابطه ذکر شده در تعریف را وقتی که لااقل یکی از این جملات درجه وجود داشته باشند بررسی خواهیم کرد.

ادامه نوشته

«تاریخچه معادلات»

معادلات همراه با اعداد، از اولین دستاوردهای ریاضی بشرند. آنها در قدیمی ترین اسناد

ریاضی، مکتوب، فی المثل، در متون میخی بابلیهای باستان، که به هزاره قبل از میلاد بر

می گردند، و پاپیروسهای مصری باستان، که به امپراطوری میانه در حدود 1800 ق.م.

بازگشت دارند، آمده اند.

بنا به ساختار جامعه بابلی مسائل مربوط به تقسیم ارث از اهمیت بسیاری برخوردار

بودند. اولین پسر همواره بیشترین سهم را دریافت می کرد، دومی بیشتر از سومی، و

به همین ترتیب.

در حالی که مسائل مطرح در بابل ،مجهول نسبتاً واضح توصیف شده است، در پاپیروس

های مصری با علامت "h" نمایش داده شده است، که توده یا گردایه را نشان می دهد.

چنین محاسباتی نسبتاً زیاد رخ می دهند و متناظر با معادلات خطی ما هستند. مقایسه

ای بین متنی مصری از پاپیروس مسکو و نماد نویسی جدید این نکته را روشن می

سازند.
پیش از این که زبان نمادین جبری مطرح شود، معادلات را بالاجبار با کلمات می نوشتند

حتی فرانسواویت که معمولاً به ویتا موسوم است که شایستگی های بسیاری در زمینه

جبر دارد از کلمه لاتین برای برابر بودن استفاده می کرد.

علامت برابری = که امروزه متداول است توسط روبرت رکورد پزشک دربار سلطنتی مطرح

شد، اما زمان قابل ملاحظه ای طول کشید تا این علامت مقبولیت عام یافت.

 

the whetstone of witte

وی این طرح را در کتاب درسی

جبری که به صورت گفتگو نوشته

شده بود و عنوانش "the

whetstone of witte" بود مطرح و

انگیزه انتخاب ان را با گفتن مطالب

زیر بیان کرد «در این مورد همان

گونه که قالباً در عمل انجام می

دهم یک جفت خط توامان می

گذارند این چنین = = =, زیرا هیچ

دو شیی نمی توانند برابر محض

باشند.

با نوشته شدن کتاب جبر و مقابله توسط خوارزمی در سده های سوم و چهارم هجری

،جبر وارد ریاضیات شد، و به حل معادله ها پرداخته شد.خود واژه جبر به معنای جبران

کردن و مقابله به معنای روبه رو قرار دادن دو سوی برابری است.
 

مجموعه جواب

کار با مجموعه معینی از اعداد، موسوم به حوزه اصلی و مجموعه مشخصی از متغیرها

که عناصری از حوزه اصلی با زیر مجموعه ای، موسوم به حوزه تغییرپذیری را می توان به

جای آنها قرارداد، آغاز می شود.

در مشخص کردن حوزه اصلی و حوزه تغییر پذیری،N به جای مجموعه اعداد طبیعی، Z به

جای مجموعه اعداد صحیح،Q به جای مجموعه اعداد گویا،R به جای مجموعه اعداد

حقیقی و C به جای اعداد مختلط قرار می گیرد.

«حل معادله روش معلوم و مجهول کردن»

جهت حل معادله یک قانون کلی داریم:

1. مجهول (x) یک طرف بقیه طرف دوم
2. اگر عددی را از یک طرف به طرف دیگر ببریم قرینه می‌شود
3. ضریب مجهول (x) / معلوم = مقدار مجهول. مثال:

 

9x+5=۱۴ برای حل جملات شامل x یک طرف نگه داشته بقیه را طرف دوم می‌بریم. اگر

عددی را از یک طرف به طرف دیگر ببریم قرینه می‌شود یعنی علامت آن برعکس می‌شود

مثبت به منفی و منفی به مثبت تبدیل می‌شود: 9x=۱۴–۵ مرحله اول در نتیجه 9x=۹

مرحله سوم: x=۹/۹=۱ پس x=۱ جواب معادله است برای امتحان معادله به جای

x درمعادله اولی مقدار بدست آمده را قرار می‌دهیم باید دو طرف معادله با هم مساوی

باشند اگر مساوی نباشند جواب بدست آمده غلط است. حال در معادله اولیه

۹x+5=۱۴ مقدار بدست آمده x=۱ را قرار می‌دهیم داریم

9x+5=14 (x=1) 9*1+5=9+5=14=14

یعنی دو طرف مساوی اند پس x=۱ جواب درست معادله است.

«حل کردن معادله»

برای حل معادله باید از خوش تعریفی توابع استفاده کرد مثلاً تابع  را بر

دو طرف تساوی اثر داده و معادله جدیدی بدست می‌آوریم مثلاً در مثال قبل بدست

می‌آوریم:

 

برای اینکه به جواب برسیم باید توابعی را اثر دهیم که تنها در یک طرف معادله باشد.

نکته مهم اینجاست که وقتی تابع یک به یک باشد جواب دو معادله با هم برابر است.

معادله چیست؟

معادله یا برابری یا هم چندی یا هَموگـِش در ریاضیات بیان برابری دو چیز با استفاده

از نماد هاست. در تمام معادله‌ها علامت تساوی (=) دیده می‌شود. هر معادله دو طرف

دارد که در دو طرف علامت تساوی ظاهر می‌شوند.

معادله دو نوع است معادله خطی  وغیر خطی. معادلاتی که مجهول آن‌ها یک می‌باشد،

معادله خطی ومعادلاتی که مجهول آنها دارای توان بیشتر از یک می‌باشد معادله غیر

خطی می‌گویند. در ریاضی معادله معمولاً بیان برابری دو عبارت است که در یکی یا

هردوی آن‌ها متغیر یا متغیرهائی وجود دارند.

معادله‌هائی که فارغ از ارزش (یا مقدار) متغیرها همواره درست باشند، اتحاد نامیده

می‌شوند. مثلاً معادله

اتحاد است چون هر چه باشد این برابری همواره درست است؛ ولی معادله

اتحاد نیست چون فقط اگر مقدار عدد ۱ باشد این برابری برقرار است. مقادیری از

متغیرها را که باعث برقراری رابطه برابری در معادله می‌شود، «جواب معادله» می‌نامند.

مثلاً در مثال قبل عدد ۱ جواب معادله است. پیدا کردن جواب معادله را «حل

معادله» می‌نامند.